L’introduction de méthodes quantitatives s’invite progressivement dans les exercices de planification financière. Motivées par la multiplication d’exercices de stress-tests et la volonté de compléter la vision à dire d’expert des opérationnels, les banques développent des modèles de projection des revenus de leurs différents métiers.
Ces projections peuvent s’appuyer sur différentes natures de modèles (mécaniques analytiques, modèles comportementaux ALM, etc.). Pour la projection des volumes d’activité, les modèles économétriques
I. L’approche statistique est au cœur de la constitution de modèles de projection
Les modèles statistiques permettent d’utiliser les historiques de mesures de performance d’une activité pour définir des relations mathématiques entre ces mesures et des variables externes (variables macroéconomiques, données du marché bancaire, etc.) ou internes (saisonnalité). Les projections consistent alors en des modèles de régression multivariée, linéaires ou non-linéaires
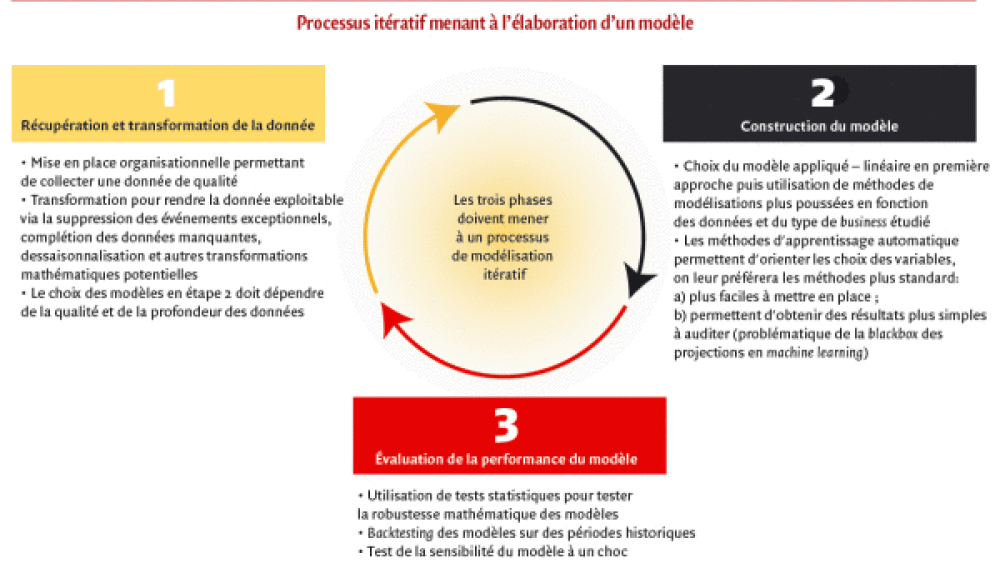
Dans le cadre de ces travaux, un compromis doit souvent être trouvé entre entre, d’une part, facilité d’implémentation et d’appropriation par les métiers et, d’autre part, puissance prédictive et robustesse statistique . La démarche pour aboutir à ce compromis consiste alors à mettre en œuvre une démarche itérative en trois étapes (comme le détaille le Schéma 1) :
1. la récupération et la transformation de la donnée;
2. la construction du modèle;
3. l’évaluation de la performance du modèle.
II. La gestion de la donnée : prérequis à la construction de modèles stables
La qualité des approches statistiques dépend fortement des données sur lesquelles s’appuient les travaux de modélisation. En effet, si les données historiques à partir desquelles sont définies les relations avec les indicateurs macroéconomiques (ou autres indicateurs) comportent des effets venant les « polluer », les modèles sont moins précis voire peuvent mener à des conclusions erronées. Dans ce contexte, la validation avec les métiers de la qualité des données est un prérequis à toute analyse statistique. Il est important d’impliquer des membres des équipes métiers dans cette réflexion afin de capter l’ensemble des éléments « non normatifs ». Une fois ces vérifications réalisées, des transformations de séries de données peuvent améliorer la qualité des modèles à tester dans l’étape (2). La pertinence de ces transformations doit tenir compte de différents types d’effets dont :
– la représentativité d’éléments business dits exceptionnels (one-offs), comme des fusions et acquisitions d’ampleur (« jumbo deals ») ou des chocs fiscaux, qui peuvent en réalité être récurrents ;
– la complétion de données manquantes et/ou asynchrones. Par exemple, on peut souhaiter projeter mensuellement un indicateur à partir de prédicteurs disponibles seulement trimestriellement. Dans ce cas, il est soit possible de s’appuyer sur des séries trimestrielles (ce qui implique de perdre des points d’analyse), soit d’interpoler mensuellement (de façon linéaire ou non), voire de réaliser un filtrage
– la saisonnalité
– le lissage de la série à expliquer, par exemple en calculant une moyenne mobile
– l’introduction d’un effet retard (ou lag) sur la série à expliquer.
D’autres transformations mathématiques pourront alternativement être appliquées sur les séries pour itérativement améliorer les résultats des modèles évalués pendant l’étape d’évaluation des modèles (3) :
– la différenciation des données (d’ordre un ou deux) avec une fréquence courte (un trimestre par exemple) ou longue (une année par exemple). Ceci permet généralement de corriger le biais statistique de la non-stationnarité
– l'application de fonctions (rendement, carré, logarithme) visant à capter des effets non linéaires ;
– l’utilisation de modèles en co-intégration (voir ci-dessous) en cas de non-stationnarité des variables à expliquer.
L’appréciation de la qualité des données collectées ainsi que les caractéristiques des transformations qui leur ont été appliquées pendant l’étape de collecte de la donnée (1) doivent être prises en compte dans le choix du modèle développé pendant l’étape de modélisation (2). En effet, la profondeur historique des données doit être suffisante pour capter des situations distinctes (crises, scénarios de taux différenciés, etc.) et les données doivent présenter des réalités métier comparables (par exemple un effet d’échelle lié au nombre de traders sur un desk ou une réorganisation de l’activité doivent être pris en compte pour harmoniser les séries d’un point de vue statistique).
III. Adapter la détermination des variables explicatives et l’expression du modèle à l’environnement
Choix du modèle
L’expression du modèle doit s’adapter aux besoins des utilisateurs de l’outil.
Les approches linéaires, par exemple, sont plus simples à mettre en œuvre mais ne permettent pas de capter des relations plus complexes qu’une relation affine entre la variable (ou sa croissance) et son inducteur (ou sa croissance). Couplées à l’utilisation de transformations non linéaires sur les variables explicatives du modèle, les approches linéaires simples permettent cependant de capter des non-linéarités. Par exemple, le logarithme des crédits immobiliers peut être corrélé au logarithme de la croissance du revenu des ménages. L’utilisation de la transformation logarithmique permet d’associer des variables dont l’ordre de grandeur est différent.
Les méthodes d’apprentissage automatique
Modèles en co-intégration
En cas de non-stationnarité, les modèles statistiques classiques sont instables et des techniques spécifiques sont à mettre en œuvre. Une notion aujourd’hui centrale est la notion de modèle en co-intégration pour des variables macroéconomiques. Un ensemble de variables est co-intégré avec la série observée s’il existe une combinaison des variables permettant d’annuler « la tendance stochastique » de la série observée pour aboutir à une série stationnaire. Par exemple, il a été démontré qu’aux États-Unis, la consommation (réelle, par habitant) et le revenu disponible (réel, par habitant) sont co-intégrés, soulignant une relation stable entre ces deux séries non stationnaires.
Ces variables co-intégrées sont alors liées avec la série observée par une équation linéaire dite « long terme » qui s’interprète comme un équilibre macroéconomique par rapport auquel les écarts constituent des fluctuations temporaires. En reprenant l’exemple précédent, une fluctuation temporaire de la consommation par rapport au revenu disponible peut survenir à un trimestre donné, mais celle-ci se répercutera avec le signe opposé sur la consommation future du prochain trimestre dans une proportion comparable, ce qui tend à ramener les deux séries vers leur point d’équilibre qui est représenté par la relation long terme.
Les approches historiques pour appréhender ce type de relation sont les approches d’Engle et Granger
Choix des variables
Dans un premier temps les variables explicatives seront choisies, parmi l’ensemble des variables transformées, grâce à des études de corrélations simples. Le choix des variables explicatives peut aussi être éclairé par l’expertise métier, des approches systématiques de classification (comme une analyse en composantes principales
Au contraire, certaines variables seront exclues a posteriori par les tests statistiques en étape (3). En particulier, un trop grand nombre de variables peut aboutir à du surcalibrage (over-fitting) et des variables colinéaires à une instabilité des coefficients de la régression
Calibrage des paramètres
La méthode d’estimation des paramètres de la régression dépend des tests réalisés en étape (3). Ils seront estimés soit par l’estimateur des moindres carrés, soit par exemple par des estimateurs de Yule-Walker
Les problèmes posés par la non-stationnarité concernent aussi l’inférence des paramètres du modèle estimé, pour laquelle les lois asymptotiques usuelles dérivées dans le cadre de séries stationnaires peuvent mener à des incohérences si utilisées telles quelles. Notamment, les p-values (voir plus bas) et les intervalles de confiances ne sont plus fiables dans le cadre des séries non-stationnaires ou de la co-intégration.
IV. L’évaluation des modèles donne sa crédibilité aux travaux de projection statistique
Le pouvoir prédictif du modèle doit être vérifié par un ensemble de tests. Des tests statistiques ou des backtestings peuvent être conduits pour conforter le choix d’un modèle, bien qu’aucun ne soit éliminatoire quant au choix du modèle. Notons que l’exigence de vérification de ces tests est à pondérer par la qualité de la donnée disponible. La sensibilité du modèle à un choc des variables explicatives devra dans tous les cas être appréciée.
Tests statistiques
Le calcul de la significativité des variables (p-value) est important mais l’estimation des paramètres et le calcul des p-valeurs doivent être corrigés en cas de non-respect des hypothèses de base de la régression linéaire
– stationnarité des séries temporelles
– résidus homoscédastiques
– normalité des résidus
Backtest (ou « cross-validation », ou « out-of-sample performance »)
Si la profondeur historique l’y autorise, il est possible de mesurer l’écart entre la série historique réelle et le modèle calibré sur une période temporelle différente. En renouvelant l’exercice sur plusieurs sous-périodes, il est possible par ailleurs de vérifier la stabilité des coefficients de la régression. Une erreur moyenne équivalente entre la période testée et la période de calibrage est un bon indicateur que le modèle n’est pas sur-calibré (over-fitting).
V. Difficultés
La modélisation de l’ensemble des agrégats financiers de la banque suppose la modélisation d’activités de natures diverses s’appuyant sur des modélisations statistiques hétérogènes. Dans ce contexte, l’équipe en charge du développement des modèles doit s’adapter à la réalité de chacun des segments d’activité. Il en résulte une panoplie de modèles statistiques à articuler sur une plateforme flexible permettant de les lier entre eux et aux sources de données (bases métier notamment) pour proposer des résultats directement exploitables par les équipes de la plateforme.
Des difficultés de quatre types doivent être dépassées pour constituer une base de modèles suffisamment solide à intégrer à la plateforme :
– la difficulté à trouver des modèles statistiques prédictifs sur certains périmètres : l’ensemble des activités ne sont pas modélisables par une approche statistique et sont plus complexes à appréhender (commissions spécifiques, frais généraux, éléments exceptionnels, etc.). Par ailleurs, la plupart des modèles statistiques classiques peinent à capter les non-linéarités dans les comportements passés ;
– l’imbrication d’effets distincts à modéliser en parallèle de la modélisation des activités : effets change, concentration des portefeuilles, etc. Les effets de contagion, de réputation et l’ensemble des « feedback effects » sont particulièrement complexes à capter ;
– la difficulté à collecter des données de qualité faciles à mettre à jour après le premier exercice de modélisation : manque de profondeur des données, problématiques d’homogénéité, etc. ;
– les difficultés organisationnelles et d’outil.
VI. Conclusion
Si les établissements bancaires disposent aujourd’hui d’équipes spécialistes de la modélisation quantitative reconnues, ces compétences se concentrent surtout dans les équipes Risques sur les problématiques de risque de crédit et de risque de marché. Pour la plupart des établissements, la modélisation prospective à partir de méthodes statistiques implique donc la constitution d’équipes spécialistes.
Les méthodes discutées plus haut apportent une vision d’ensemble des moyens statistiques dont disposent les équipes de planification pour construire des modèles de projection. La dimension humaine et la capacité à recruter des talents capables de construire des modèles complexes sont au cœur des enjeux.
Le développement d’une approche tactique, via des outils agiles, permet dans un premier temps de constituer un premier support à la plateforme et de distinguer la construction des modèles de leur industrialisation dans les systèmes de la banque.
-
1 Les modèles économétriques permettent la modélisation de variables économiques à partir de l’observation statistique de grandeurs pertinentes. -
2 Les modèles de régression permettent d’expliquer l’évolution d’une variable en fonction d’une (modèle univarié) ou plusieurs variables (modèle multivarié). Ces modèles de régression peuvent être linéaires s’il existe une relation de proportionnalité directe entre la variable expliquée et les variables explicatives. -
3 Ceci peut être implémenté à l’aide d’un filtre de Kalman par exemple. -
4 Ou plus généralement l’autocorrélation de la série, ce qui revient à introduire une variable endogène dans le modèle. -
5 L’algorithme ARIMA-X12 est une méthode populaire d’ajustement de la saisonnalité développée par le Bureau du recensement des États-Unis. Cette méthode s’applique à des séries ayant une saisonnalité mensuelle ou trimestrielle. Elle est implémentée dans la plupart des logiciels de statistiques et est l’une des méthodes prônées par l’European Statistical System (ESS). -
6 La procédure STL (“Seasonal and Trend decomposition using Loess”) est une méthode de décomposition d’une série temporelle en une composante saisonnière, une tendance et des résidus. A ce titre, c’est aussi une méthode d’ajustement de la saisonnalité qui peut être préférée dans certains cas à des méthodes du type ARIMA-X12 (notamment en cas de composante saisonnière fluctuante ou en présence d’observations aberrantes). -
7 Plus généralement, cela peut être incorporé, avec la saisonnalité, dans une démarché de modélisation de type ARMA (Auto Regressive Moving Average), ARIMA (AutoRegressive Integrated Moving Average) ou SARIMA (Seasonal ARIMA). -
8 Le caractère stationnaire (ou non) d’une série temporelle se rapporte à l’homogénéité de sa distribution statistique au cours du temps. Une propriété plus faible utilisée en pratique (stationnarité faible) est le fait d’avoir ses deux premiers moments (moyenne et variance) constants, ainsi qu’une fonction d’autocorrélation invariante par translation au cours du temps. -
9 Ces méthodes font partie de ce que l’on appelle aujourd’hui le « Machine Learning » qui vise à tirer parti des données pour déterminer la forme du modèle à adopter, plutôt que de le spécifier en amont. Ces méthodes se fondent sur l’analyse statistique d’un grand nombre de données de natures variées. -
10 Les forêts aléatoires sont une famille d’algorithmes d’apprentissage automatique qui se fondent sur des ensembles d’arbres de décision. L’intérêt de cette méthode est d’entraîner un ensemble d’arbres de décision sur des sous-ensembles de l’ensemble des données initiales et ainsi de limiter le problème de sur apprentissage. Ce type d’algorithme permet de faire de la classification (estimation de variables discrètes) mais aussi de la régression (estimation de variables continues). -
11 Un modèle autorégressif est un modèle dans lequel une variable est expliquée par ses valeurs passées plutôt que par d’autres variables. -
12 Co-Integration and Error Correction: Representation, Estimation, and Testing, Robert F. Engle and C. W. J. Granger, 1987. -
13 Estimation and Hypothesis Testing of Cointegration Vectors in Gaussian Vector Autoregressive Models, Johansen, Søren, 1991. -
14 L'analyse en composantes principales (ACP), est une méthode d'analyse de données, qui consiste à transformer des variables corrélées entre elles en nouvelles variables dé-corrélées les unes des autres à partir de leurs caractéristiques mathématiques (décomposition orthogonale aux valeurs propres). -
15 Les régressions Lasso ou Ridge permettent de régulariser le problème et de sélectionner les variables de plus d’intérêt en introduisant des termes de pénalité. -
16 Les équations de Yule-Walker établissent une correspondance directe entre les paramètres du modèle et ses autocovariances. Elles sont utiles pour déterminer la fonction d'autocorrélation ou estimer les paramètres d’un modèle. -
17 Quand les hypothèses qui fournissent les distributions asymptotiques ou les intervalles de confiance des estimateurs ne sont plus vérifiées, les intervalles de confiance peuvent quand même être calculés par simulation (bootstraping ou ré échantillonnage). -
18 Les tests classiques à mener sont ceux de Dickey-Fuller (augmenté), Phillips-Perron ou Kwiatkowski-Phillips-Schmidt-Shin. -
19 Tests de Breusch-Pagan et de Goldfeld et Quandt. -
20 Tests de Durbin-Watson et de Breusch-Godfrey. -
21 Transformation de Yule-Walker (Cochrane-Orcutt généralisé). -
22 Correction de la matrice de covariance par l’estimateur de Newey-West. -
23 Test de Shapiro-Wilk par exemple.






![[Web Only] Tarifs bancaires : les banques amortissent l’inflation [Web Only] Tarifs bancaires : les banques amortissent l’inflation](http://www.revue-banque.fr/binrepository/480x320/0c0/0d0/none/9739565/MEBW/gettyimages-968963256-frais-bancaires_221-3514277_20240417171729.jpg)




